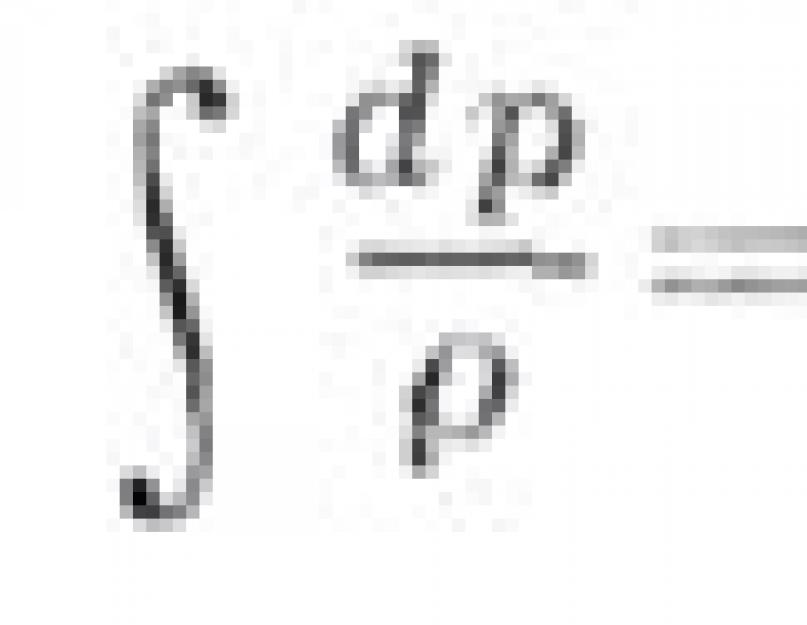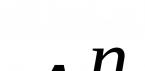уравнений гидродинамики - интеграл, определяющий давление рв каждой точке установившегося потока идеальной однородной жидкости или баротропного газа через скорость потока в соответствующей точке и через силовую функцию объемных сил:

Постоянная Симеет для каждой линии тока свое значение, меняющееся при переходе от одной линии тока к другой. Если движение потенциальное, то постоянная Сдля всего потока одна и та же.

Для неустановившегося движения Б. и. (наз. иногда интегралом Коши - Лагранжа) имеет место при наличии потенциала скоростей:

и есть произвольная функция времени.

Для несжимаемой жидкости левая часть уравнений (1), (2) приводится к виду ; для баротропного газа - к виду:

Б. и. предложен Д. Бернулли (D. Bernoulli, 1738). Лит. : Мил н-Томсон Л. М., Теоретическая гидродинамика, пер. с англ., М., 1964. Л. Н. Сретенский.

• - Даниил, швейц. учёный, чл. Петерб. АН. Проф. ун-та в Базеле. В 1725-33 работал в России. Одним из первых использовал методы теории вероятностей при рассмотрении ряда вопросов количеств, изучения нас. В работе "...
• - Кристоф, швейц. учёный, проф. технич. наук ун-та в Базеле...

  Демографический энциклопедический словарь

• - автоморфизм пространства с мерой:, описывающий Бернулли испытания и их обобщение - последовательность независимых испытаний, имеющих одни и те же исходы и одно и то же распределение вероятностей...

  Математическая энциклопедия

• - случайное блуждание, порождаемое Бернулли испытаниями. На примере Б. б. можно пояснить нек-рые основные черты более общих случайных блужданий...

  Математическая энциклопедия

• - независимые испытания с двумя исходами каждое и такие, что вероятности исходов не изменяются от испытания к испытанию. Б. и. служат одной из основных схем, рассматриваемых в теории вероятностей...

  Математическая энциклопедия

• - плоская алгебраич...

  Математическая энциклопедия

• - метод нахождения наибольшего по абсолютной величине действительного корня алгебраич. уравнения вида Предложен Д. Бернулли; состоит- в следующем. Пусть - произвольно выбранные числа...

  Математическая энциклопедия

• - многочлены вида где Bs- Бернулли числа...

  Математическая энциклопедия

• - то же, что биномиальное распределение...

  Математическая энциклопедия

• - правило, согласно котором у сила сокращения мышцы при прочих равных условиях пропорциональна длине ее мышечных волокон, т. е. степени ее предварительного растяжения...

  Большой медицинский словарь

• - Даниэль, швейцарский математик и физик, член знаменитой семьи математиков. В своих трудах по гидродинамике показал, что давление жидкости уменьшается по мере возрастания скорости ее течения...

  Научно-технический энциклопедический словарь

• - династия швейцарских ученых родом из Антверпена, бежавших из города после захвата его испанцами и поселившихся в 1622 в Базеле...

  Энциклопедия Кольера

• - семейство, давшее ряд замечательных людей, преимущественно в области математических наук. Родоначальник его Яков Б. эмигрировал из Антверпена во время управления Фландрией герцога Альбы, во Франкфурт...

  Энциклопедический словарь Брокгауза и Евфрона

• - семья швейцарских учёных, родоначальник которой Якоб Б. был выходцем из Голландии. Якоб Б. , профессор математики Базельского университета...

  Большая Советская энциклопедия

• - семья швейцарских ученых, давшая видных математиков...

  Большой энциклопедический словарь

• - Берн"улли, нескл., муж.: сх"ема Берн"улли, теор"ема Берн"улли, уравн"ение Берн"улли, ч"исла Берн"...

  Русский орфографический словарь

"БЕРНУЛЛИ ИНТЕГРАЛ" в книгах

Вызов Бернулли

Из книги Больше, чем вы знаете. Необычный взгляд на мир финансов автора Мобуссин Майкл

Вызов Бернулли Компетентные инвесторы гордятся своей способностью определять правильную цену финансовых заявок. Эта способность является сутью инвестирования: рынок – лишь средство для обмена денег на будущие заявки и наоборот.Хорошо, вот вам ситуация для оценки:

11. ИНТЕГРАЛ В ЛОГИКЕ

Из книги Хаос и структура автора Лосев Алексей Федорович

11. ИНТЕГРАЛ В ЛОГИКЕ Как мы знаем, интегрирование определяется в математике или в качестве процесса, обратного дифференцированию, или в качестве нахождения предела суммы. В первом смысле интегрирование для нас менее интересно, так как здесь мы имеем дело с прямым

ИНТЕГРАЛ

Из книги Русский рок. Малая энциклопедия автора Бушуева Светлана

ИНТЕГРАЛ Эта «кузница кадров» возникла в городе Усть-Каменогорске в конце 80-х годов. В «Интеграле» в разное время переиграли: Юрий Лоза, Игорь Сандлер, Юрий Ильченко, Игорь Новиков, Ярослав Ангелюк, Женя Белоусов, Марина Хлебникова и другие. В начале 80-х группа играла

Бернулли

Из книги Энциклопедический словарь (Б) автора Брокгауз Ф. А.

Бернулли Бернулли (Bernoulli) – семейство, давшее ряд замечательных людей, преимущественно в области математических наук. Родоначальник его Яков Б. (ум. 1583 г.), эмигрировал из Антверпена вовремя управления Фландрией герцога Альбы во Франкфурт; внук его, также Яков Б, род. 1598 г.,

Бернулли

БСЭ

Бернулли схема

Из книги Большая Советская Энциклопедия (БЕ) автора БСЭ

Бернулли схема Бернулли схема (названа по имени Я. Бернулли), одна из основных математических моделей для описания независимых повторений опытов, используемых в вероятностей теории. Б. с. предполагает, что имеется некоторый опыт S и связанное с ним случайное событие А

Бернулли теорема

Из книги Большая Советская Энциклопедия (БЕ) автора БСЭ

автора Канеман Даниэль

Ошибки Бернулли В начале 1970-х годов Амос вручил мне брошюру швейцарского экономиста Бруно Фрея, где обсуждались психологические аспекты экономической теории. Я помню даже цвет обложки - темно-красный. Бруно Фрей почти и не вспоминает эту статью, но я все еще могу по

Ошибка Бернулли

Из книги Думай медленно... решай быстро автора Канеман Даниэль

Ошибка Бернулли Как хорошо понимал Фехнер, он не первый пытался найти функцию, связывающую психологическую интенсивность с физической силой стимула. В 1738 году швейцарский ученый Даниил Бернулли предвосхитил объяснения Фехнера и применил их к отношениям между

25. Уравнение Бернулли

Из книги Гидравлика автора Бабаев М А

25. Уравнение Бернулли Уравнение Громеки подходит для описания движения жидкости, если компоненты функции движения содержат какуююто вихревую величину. Например, эта вихревая величина содержится в компонентах?x, ?y,?z угловой скорости w.Условием того, что движение

1.4. Уравнения энергии

Уравнение и интеграл Бернулли. Решение уравнений Эйлера (1.76) приводит к одному из наиболее важных уравнений гидродинамики  уравнению Бернулли. Умножим первое из уравнений Эйлера (1.76) на dx , второе  на dy , третье  на dz , а затем почленно сложим. В результате получим

Проинтегрируем (1.108) вдоль элементарной струйки при следующих допущениях:

Рассмотрим отдельные суммы, входящие в (1.108).

Учитывая, что
,
,
, представим сумму в левой части в виде

, (1.109)

где u  действительная полная скорость в данной точке.

На основании второго и третьего допущений проекции ускорений массовых сил на оси координат составят X = Y = 0, Z =- g . Тогда первая сумма в правой части (1.108) примет вид

Xdx + Ydy + Zdz =- gdz . (1.110)

В силу первого допущения все параметры потока, в том числе и давление, не зависят от времени и являются функциями только координат, т. е. p = p (x , y , z ). Следовательно, выражение в скобках у второго слагаемого в правой части (1.108) является полным дифференциалом давления, т. е.

. (1.111)

Подставляя (1.109), (1.110), (1.111) в (1.108) и собирая все слагаемые в левой части, получим

. (1.112)

Выражение (1.112) называют дифференциальным уравнением Бернулли.

Единица измерения членов уравнения (1.112)  Дж/кг.

Уравнение Бернулли можно представить в других видах, умножив все его члены на ρ ,

(1.113)

или разделив на g

. (1.114)

При этом единицы измерения всех членов уравнения (1.113)  Па, а (1.114)  м.

Проинтегрировав уравнения (1.112)  (1.114), получим выражения

; (1.115)

; (1.116)

. (1.117)

Уравнения (1.115)-(1.117) называются интегралом Бернулли.

Энергетический смысл интеграла Бернулли . Принимая ρ = const, в результате интегрирования уравнения (1.112) получим

const. (1.118)

Единица измерения всех членов уравнения (1.118), так же как и (1.112)  Дж/кг.

Движущаяся частичка жидкости обладает вполне определенным запасом механической энергии. Если абсолютно твердое тело обладает запасом потенциальной энергии положения в поле сил тяжести и кинетической энергией, то жидкая частичка, как упругое тело, обладает еще и запасом потенциальной энергии состояния. Эта энергия тем больше, чем больше объем жидкости и чем выше давление, и проявляется в том, что, например, нагнетание жидкости в сосуд может привести к разрушению сосуда, а сжатый газ может совершать работу при расширении.

Следовательно, полная механическая энергия жидкой частички Э может быть определена как сумма Э = П п +П с +К , где П п  потенциальная энергия положения в поле сил тяжести; П с  потенциальная энергия состояния; К  кинетическая энергия.

Потенциальная энергия положения может быть подсчитана по общей формуле механики П п = mgz , где m  масса жидкой частички, кг; z  высота ее положения над горизонтальной плоскостью отсчета, м.

Рассмотрим удельную энергию, приходящуюся на единицу массы жидкости. Удельная потенциальная энергия положения составляет
и в интеграле Бернулли (1.118) представлена первым слагаемым.

Потенциальная энергия состояния вычисляется по формуле П с = pV , где p  давление, Па; V  объем жидкой частички, м 3 .

Удельная потенциальная энергия состояния
в интеграле Бернулли (1.118) представлена вторым слагаемым.

Кинетическая энергия жидкой частички
.

Удельная кинетическая энергия
в интеграле Бернулли (1.118) представлена третьим слагаемым.

Полная механическая энергия жидкой частички определяется, следовательно, суммой
, а удельная механическая энергия составит

. (1.119)

Сравнивая (1.118) и (1.119), приходим к энергетическому смыслу интеграла Бернулли: удельная механическая энергия идеальной несжимаемой жидкости остается постоянной вдоль элементарной струйки. Таким образом, интеграл Бернулли выражает собой закон сохранения механической энергии для элементарной струйки, т. е. является энергетическим уравнением.

Из интеграла Бернулли следует также вывод о том, что отдельные составляющие удельной механической энергии могут изменяться, но при этом происходит преобразование одного вида энергии в другой, т. е. уменьшение одного слагаемого обязательно должно сопровождаться увеличением хотя бы одного из двух остальных и наоборот.

Сумма членов интеграла Бернулли (1.115) дает полный запас энергии, которым обладает единица массы (e ), (1.116)  единица объема (p ), (1.117)  единица силы тяжести относительно принятой плоскости сравнения (H ).

Члены , , выражают кинетическую энергию, суммы
,
,
 потенциальную энергию, где gz , ρgz , z  потенциальная энергия положения, а , ,  потенциальная энергия состояния соответственно единицы массы, объема, единицы силы тяжести. Можно также сказать, что уравнения (1.116) и (1.117) выражают собой то же, что и уравнение (1.99), но в масштабе и
соответственно.

Уравнением (1.115) удобно пользоваться при исследовании движения газа с переменной плотностью, например, в пневмосетях и компрессорах.

Если при движении газа изменения давления незначительны
и температура постоянна, то можно считатьρ = const. В этих условиях удобно пользоваться уравнением (1.116), которое примет вид

const. (1.120)

Выражением (1.120) удобно пользоваться при исследовании движения воздуха в вентиляционных сетях и вентиляторах.

При движении капельной жидкости (воды, масла и т. п.), плотность которой постоянна, удобнее всего пользоваться уравнением (1.117), которое для ρ = const примет вид

const. (1.121)

Уравнение (1.121) применяется при расчетах водопроводов, гидромагистралей, насосов.

Часто употребляется иная запись уравнения (1.117). Обозначая индексом 1 параметры потока в первом по ходу движения жидкости сечении струйки, а индексом 2  в последующем, можем записать

. (1.122)

Геометрический смысл уравнения Бернулли. Все слагаемые уравнения (1.122) имеют размерность длины, поэтому можно говорить о геометрическом смысле уравнения Бернулли: z  геометрическая (геодезическая, нивелирная) высота;
 пьезометрическая высота;
 скоростная (динамическая) высота;  высота потерь энергии (напора).

Приведем иные названия: z  геометрический напор;
 пьезометрический напор;
 скоростной напор;  потеря напора;
 полный напор.

Рассмотрим поток жидкости в канале, измеряя все слагаемые уравнения Бернулли (1.122) в различных сечениях (Рис. 1.30, показаны замеры лишь для двух сечений 1-1 и 2-2 ). За плоскость отсчета примем произвольную горизонтальную плоскость 0-0 .

Г

Рис. 1.30. Геометрическая интерпретация уравнения Бернулли

еометрические высотыz легко определяются как расстояние по вертикали от плоскости отсчета до центров тяжести соответствующих сечений. Пьезометрические высоты
определяются как высоты поднятия жидкости в пьезометрах, отсчитанные по вертикали от центров тяжести соответствующих сечений. Скоростные высоты
определяются как разности уровней жидкости в трубках Пито и пьезометрах, помещенных в соответствующие сечения (необходимо отметить, что для точного измерения величины
трубку Пито следует помещать в такую точку сечения, где локальная скоростьu равна средней скорости v , что не всегда можно сделать, ибо положение этой точки редко известно).

Высота потерь энергии на участке, ограниченном сечениями 1-1 и 2-2 , определится как разность уровней жидкости в трубках Пито, помещенных в эти сечения.

Если аналогичные измерения выполнить для множества промежуточных сечений и соединить плавной линией верхние мениски жидкости в трубках Пито, то мы получим линию a (см. Рис. 1.30), которую называют линией полного напора .

Соединяя плавной линией верхние мениски жидкости в пьезометрах мы получим линию b (см. Рис. 1.30), которую называют пьезометрической линией .

Линию, соединяющую центры тяжести сечений, называют осью потока .

Характер поведения этих линий по длине потока l определяется так называемыми уклонами.

Гидравлическим уклоном называют величину

, (1.123)

определяющую поведение линии полного напора.

Пьезометрический уклон

, (1.124)

определяет поведение пьезометрической линии.

Геометрический (геодезический) уклон

, (1.125)

характеризует поведение оси потока.

В практических расчетах чаще используются средние значения уклонов, вычисляемые как отношение разностей соответствующих величин в начале и конце к длине потока.

Так как вдоль по потоку полная энергия его за счет потерь непрерывно уменьшается, то линия полного напора всегда понижается. Гидравлический уклон (1.124) всегда остается положительным.

Пьезометрическая линия может и понижаться, и повышаться. Ее поведение зависит как от потерь напора, так и от характера изменения кинетической энергии. При расширении канала скорость потока и скоростной напор уменьшаются. Если скорость уменьшения скоростного напора окажется выше, чем скорость уменьшения полного напора, то пьезометрическая линия будет подниматься.

Диаграммы напоров. В ряде задач гидравлики целесообразно бывает дать графическое изображение уравнения Бернулли для того или иного канала. Такие графики называют диаграммами напора. Они позволяют очень наглядно анализировать поведение каждого слагаемого в уравнении Бернулли при течении жидкости по каналу. С их помощью удобно также производить некоторые числовые расчеты. Обычно диаграммы строят по результатам конкретных расчетов, откладывая в масштабе для каждого сечения значения напоров. Рассмотрим принцип построения диаграммы.

Рис. 1.31. Диаграмма напоров

Пусть из открытого сосуда больших размеров жидкость вытекает в атмосферу по трубе переменного сечения (Рис. 1.31). Выберем в качестве плоскости отсчета произвольную горизонтальную плоскость 0-0. Построение диаграммы начнем с линии полного напора.

Для этого определим полный напор в сечении, совпадающем со свободной поверхностью жидкости в сосуде. Условимся в уравнении Бернулли и при построении пользоваться избыточными давлениями. Тогда на свободной поверхности
.

Так как площадь сосуда значительно превосходит площадь сечения трубы, то в соответствии с уравнением расхода скорость жидкости в сосуде будет очень мала по сравнению со скоростью в трубе, а следовательно, можно пренебречь скоростным напором
.

Таким образом, полный напор определяется лишь геометрическим напором (на диаграмме он отмечен точкой a ). Полные напоры в последующих сечениях будем оценивать как разность полного напора в предыдущем сечении и потерь напора на участке между этими сечениями

. (1.126)

Забегая несколько вперед, отметим, что различают два вида потерь напора: потери на трение, обусловленные вязкостью жидкости и местные потери, обусловленные резким изменением конфигурации потока, которые в отличие от потерь на трение (путевых) принято считать сосредоточенными в одном сечении потока. Потери на трение тем больше, чем больше длина канала и скорость потока и чем меньше сечение (диаметр) канала.

В сечении 1-1 сразу за входом потока из сосуда в трубу полный напор будет меньше напора в сосуде на величину местных потерь входа. Вычитая из полного напора в сосуде (точка a ) потери входа h 1 , получим точку b , определяющую полный напор в сечении 1-1.

На участке трубы между сечениями 1-1 и 2-2 будут происходить потери напора на трение. Так как труба на этом участке имеет постоянное сечение, то везде на единицу длины приходятся одинаковые потери, т. е. график полного напора будет иметь линейный характер. Вычитая из полного напора в сечении 1-1 величину потерь напора на трение на участке h 2 , получим полный напор в сечении 2-2 (точка с ). Соединив точки b и с прямой линией, получим график полного напора для первого участка трубы.

По аналогии с входом в трубу, вычитая из полного напора в сечении 2-2 (точка с ) местные потери при внезапном расширении потока h 3 , получим полный напор в сечении 3-3 за внезапным расширением (точка d ), вычитая из которого потери на трение на втором участке трубы h 4 , получим полный напор в выходном сечении 4-4 (точка е ).

При соединении точек d и е необходимо учесть, что потери на трение на единицу длины (гидравлический уклон) в начале участка (большие диаметры) будут меньше, чем в конце (малые диаметры). Следовательно, линия полного напора будет направлена выпуклостью вверх. Таким образом, получили линию полного напора abcde .

Перейдем теперь к построению пьезометрической линии. С этой целью из полного напора в каждом сечении будем вычитать скоростной напор, т. к.

. (1.127)

На свободной поверхности жидкости в сосуде скоростной напор равен нулю и пьезометрический напор совпадает с полным (точка а ).

На участке между сечениями 1-1 и 2-2 сечение трубы, скорость и скоростной напор остаются постоянными, и пьезометрическая линия (
) будет параллельна линии полного напора.

При переходе от сечения 2-2 к сечению 3-3 происходит резкое увеличение сечения, сопровождающееся уменьшением скорости и скоростного напора. Поэтому пьезометрический напор в сечении 3-3 определиться вычитанием из полного напора значительно меньшей величины (отрезок
), чем для сечения 2-2 (отрезок).

На втором участке трубы сечение постепенно уменьшается, что приводит к постепенному возрастанию скорости и скоростного напора. Следовательно, в каждом последующем сечении из полного напора необходимо вычитать все большую и большую величину. Поэтому пьезометрическая линия непрерывно удаляется от линии полного напора. Заканчивается пьезометрическая линия в точке , совпадающей с центром тяжести выходного сечения 4-4. Это объясняется тем, что в выходном сечении снова действует атмосферное давление и пьезометрический напор
по избыточному давлению равен нулю. Полный же напор складывается из геометрического и скоростного.

По аналогии с построением диаграммы напора по заданному профилю потока возможно решение и обратной задачи: построение конфигурации трубопровода по заданным диаграммам напора.

Примеры практического использования уравнения Бернулли . Уравнение Бернулли позволяет получить расчетные формулы для различных случаев движения жидкости и решить многие практические задачи. При этом следует иметь в виду, что оно справедливо только для установившихся потоков с плоскими живыми сечениями.

Для практического использования уравнения Бернулли при решении различных задач проводят два сечения и горизонтальную плоскость  плоскость сравнения. Последнюю, чтобы было меньше неизвестных, проводят через центр тяжести одного или, если это возможно, двух сечений, и тогда z 1 или z 2 (или оба) будут равны нулю. Сечения проводят нормально к направлению движения жидкости, а места их проведения выбирают так, чтобы сечения были плоскими, содержали неизвестные величины, подлежащие определению, и достаточное число известных величин. Обычно такими местами являются свободная поверхность жидкости, вход или выход из трубопровода, места подключения измерительных приборов и пр. Далее для выбранных сечений, которые нумеруются по ходу движения жидкости, записывается уравнение Бернулли, подставляются в него числовые значения величин и вычисляются искомые.

При решении некоторых задач приходится дополнительно использовать условие неразрывности (сплошности) течения и брать более двух сечений.

В уравнение Бернулли подставляются абсолютные давления. Покажем это на простейшем примере (Рис. 1.32). Пусть требуется определить скорость истечения жидкости из резервуара через отверстие в стенке при постоянном напоре (уровень жидкости в резервуаре постоянен).

П

Рис. 1.32. Истечение жидкости из отверстия

роводим сечение 1-1 по уровню жидкости в резервуаре и сечение 2-2 на выходе струи из отверстия. Проводим произвольную горизонтальную плоскость сравненияx 0 y . Известными величинами являются z 1 , z 2 (z 1 - z 2 = h ), p 1 = p 2 = p a (резервуар открыт и истечение происходит в атмосферу). Тогда, пренебрегая незначительными потерями напора при выходе струи из отверстия и принимая коэффициент  = 1, из уравнения (1.122) находим
.

Измерение давлений и локальных скоростей. Покоящаяся жидкость не обладает кинетической энергией. Тогда интеграл Бернулли (1.118) примет вид

const. (1.128)

Обозначив давление на свободной поверхности жидкости p 0 , а ее координату z 0 (Рис. 1.33), уравнению (1.128) можем придать вид

или
. (1.129)

О

Рис. 1.33. Измерение давлений пьезометрами

бозначив глубину погружения точки (например,А ) под свободной поверхностью жидкости через h = z 0 - z , придадим (1.129) вид
.

Последнее является основным уравнением гидростатики (1.26) и было получено ранее решением дифференциальных уравнений равновесия Эйлера.

Введем в точку В (Рис. 1.33) закрытый пьезометр , представляющий собой стеклянную трубку с запаянным верхним концом из которой удален воздух. Под действием давления в точке В жидкость поднимается на некоторую высоту h ’ . Для ее вычисления запишем (1.26) для покоящейся жидкости в пьезометре. Так как из него удален воздух, то над жидкостью давление будет равно нулю.

, (1.130)

. (1.131)

Таким образом, высота поднятия жидкости в пьезометре в некотором масштабе (1:g ) определяет удельную потенциальную энергию состояния жидкости, а выражение (1.131) можно использовать для расчета давления, измеренного с помощью пьезометра. Формула (1.131) определяет способ пересчета давлений, выраженных высотой столба жидкости, в размерные единицы.

Так как (1.26) получена на основании (1.130), то легко видеть, что в какую бы точку данной покоящейся жидкости мы ни помещали пьезометр, сумма координаты z этой точки и высоты подъема жидкости в пьезометре остается постоянной, т. е. верхний мениск жидкости в пьезометре всегда будет находиться на одном и том же уровне. Горизонтальную плоскость a - a (Рис. 1.33), проведенную через верхние мениски жидкости в пьезометрах, называют напорной плоскостью , построенной по абсолютному давлению.

Закрытый пьезометр, как видим, измеряет абсолютное давление в жидкости. Избыточное давление можно измерить с помощью открытого пьезометра , представляющего собой стеклянную трубку, открытую с обоих концов.

Поместим открытый пьезометр (см. Рис. 1.33) в точку, расположенную на той же глубине под свободной поверхностью, что и точкаВ . Из (1.26) видно, что давления в точках иВ будут одинаковы.

Над свободной поверхностью жидкости в пьезометре будет действовать атмосферное давление, поэтому на основании (1.26) можем написать
, откуда

, (1.132)

т. е. высота поднятия жидкости в открытом пьезометре в масштабе (1:g ) измеряет ту же удельную потенциальную энергию состояния жидкости, но определенную по избыточному давлению.

С

Рис. 1.34. Измерение локальных скоростей трубкой Пито-Прандтля

казанное выше об уровнях жидкости в закрытых пьезометрах справедливо и для открытых, с той лишь разницей, что напорная плоскость по избыточному давлению
(см. Рис. 1.33), проведенная через верхние мениски жидкости в открытых пьезометрах, будет расположена ниже плоскости a - a на высоту
, в чем нетрудно убедиться с помощью (1.132) и (1.133).

Для измерения локальных скоростей в закрытых каналах, движение жидкости в которых называют напорным, используется трубка Пито-Прандтля, представляющая собой комбинацию трубки Пито и пьезометра (Рис. 1.34), которые обычно объединяются в одну конструкцию.

Трубка Пито-Прандтля вводится в поток таким образом, чтобы открытый конец трубки Пито был направлен перпендикулярно к вектору скорости, а открытый конец пьезометра  по касательной.

Как и в предыдущем случае, для трубки Пито справедливо условие

, (1.133)

только высота h и имеют здесь иной смысл (см. Рис. 1.34).

Поскольку жидкость проскальзывает около входного сечения пьезометра не затормаживаясь, то в нем будет действовать такое же давление, как и в движущейся жидкости, т. е. . Для него на основании (1.70) можем написать (т. к. на свободной поверхности жидкости в пьезометре действует атмосферное давление, как и в трубке Пито) уравнение

Выделяют отраслевые и интегральные промышленные районы.

Графическое представление и практическое применение уравнения Бернулли

Графическое представление уравнения Бернулли для потока идеальной и реальной жидкости.

Графическое представление уравнения Бернулли для струйки идеальной и реальной жидкости.

Бернулли уравнение одно из основных уравнений гидромеханики, которое при установившемся движении несжимаемой идеальной жидкости в однородном поле сил тяжести имеет вид:
Gh + p/ρ + v 2 /2 = C, (1)
где v - скорость жидкости, ρ - её плотность, р - давление в ней, h - высота жидкой частицы над некоторой горизонтальной плоскостью, g - ускорение свободного падения, С - величина, постоянная на каждой линии тока, но в общем случае изменяющая своё значение при переходе от одной линии тока к другой.

Сумма первых двух членов в левой части уравнения (1) равна полной потенциальной, а третий член - кинетической энергиям, отнесённым к ед. массы жидкости; следовательно, всё уравнение выражает для движущейся жидкости закон сохранения механической энергии и устанавливает важную зависимость между v, p и h. Например, если при неизменной h скорость течения вдоль линии тока возрастает, то давление падает, и наоборот. Этот закон используют при измерении скорости с помощью трубок измерительных и при других аэродинамических измерениях.

Уравнение Бернулли представляют также в виде
h + p/γ + v 2 /2g = C или
γh + p + ρv 2 /2 = C (2)
(где γ =ρg - удельный вес жидкости). В 1-м равенстве все слагаемые имеют размерность длины и называются соответствующей геометрической (нивелирной), пьезометрической и скоростной высотами, а во 2-м - размерности давления и соответственно именуются весовым, статическим и динамическим давлениями.

В общем случае, когда жидкость является сжимаемой (газ), но баротропной, т. е. р в ней зависит только от ρ, и когда её движение происходит в любом, но потенциальном поле объёмных (массовых) сил (см. Силовое поле), уравнение Бернулли получается как следствие Эйлера уравнений гидромеханики и имеет вид:
П+∫ dp/ρ + v 2 /2 = C, (3)
где П - потенциальная энергия (потенциал) поля объёмных сил, отнесённая к ед. массы жидкости. При течении газов значение П мало изменяется вдоль линии тока, и его можно включить в константу, представив (3) в виде:
∫ dp/ρ + v 2 /2 = C. (4)

В технических приложениях для течения, осреднённого по поперечному сечению канала, применяют т. н. обобщённое уравнение Бернулли: сохраняя форму уравнений (1) и (3), в левую часть включают работу сил трения и преодоления гидравлических сопротивлений, а также механическую работу жидкости или газа (работу компрессора или турбин) с соответствующим знаком. Обобщённое уравнение Бернулли широко применяется в гидравлике при расчёте течения жидкостей и газов в трубопроводах и в машиностроении при расчёте компрессоров, турбин, насосов и других гидравлических и газовых машин.

Интеграл Бернулли.

Придадим уравнению количества движения иную форму. Для этого воспользуемся известной формулой вектор­ного анализа

положив в ней . Следовательно, справедливо равенство

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, уравнение количества движения приобретет вид уравнения Громеки – Лэмба

(2.79)

Как мы убедимся в дальнейшем, эта форма уравнения чрезвы­чайно удобна для анализа течения идеальной жидкости.

Рассмотрим сначала случай стационарного течения, т. е. поло­жим , и умножим (2.48) скалярно на вектор . Тогда по­лучим

(2.80)

Так как массовые силы имеют потенциал П, то

Вместе с тем, пусть существует функция давления

Течения, в которых плотность зависит только от давления, на­зываются баротропными. Градиент функции , равный

может рассматриваться как вектор объёмного действия поверх­ностных сил, а сама функция как потенциал объёмно­го действия поверхностных сил .

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, (2.80) дает

Сумму, стоящую в скобках, называют трехчленом Бернулли и обозначают как В : .

Итак, , где означает производную, взятую вдоль линии тока. Отсюда следует, что B=const или

(2.83)

Напомним, что это соотношение справедливо вдоль линии тока. При переходе от одной линии тока к другой константа͵ в принципе, может изменяться. Равенство (2.83) будет справедливо по всœей области течения, в случае если , что возможно при или при .

Равенство (2.83) носит название интеграла Бернулли . Соотно­шение (2.83) часто называют также теоремой (уравнением) Бернулли .

В гидромеханике (и особенно в гидравлике) наиболее распрост­раненным является случай интеграла Бернулли для несжимаемой жидкости. Положим ρ=const . Тогда . Будем считать, что жидкость находится только под действием сил тяжести, т. е. , где y – ось, направленная вертикально вверх. Та­ким образом, теорема Бернулли принимает следующую форму:

(2.84)

В случае если поделить всœе члены на ускорение силы тяжести g и обо­значить константу через Н*, то можно записать

, (2.85)

где – удельный вес; Н* – гидравлическая высота͵

и дать теореме Бернулли классическую формулировку:

при стационарном движении тяжелой идеальной несжимаемой жидкости гидравлическая высота Н* , равная сумме скоростной , пьезометрической и нивелирной у высот, сохраняет посто­янное значение вдоль любой линии тока (или вихревой линии).

В пренебрежении силами тяжести теореме Бернулли можно при­дать более простой вид:

(2.86)

Первый член левой части называют пьезометрическим напором или статическим давлением, второй – скоростным напором или ди­намическим давлением. Правая часть представляет собой полный напор или давление торможения.

Рассмотрим теперь адиабатическое течение воды в рамках невесомой идеальной жидкости. В соответствии с уравнением Тэйта будем иметь

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, теорема Бернулли для сжимаемой воды будет выглядеть так:

(2.87)

Предположим, что параметры жидкость приобретает в точке, где скорость обращается в нуль. В случае если в действительности такая точка отсутствует, то можно представить себе воображаемое движение идеальной сжимаемой жидкости, адиабатически её за­тормаживающее. Величины и в данном случае называются соответственно давлением и плотностью торможения. При сделанном предположении уравнение (2.87) примет вид

(2.88)

Интеграл Бернулли. - понятие и виды. Классификация и особенности категории "Интеграл Бернулли." 2017, 2018.

Предположим, что жидкость идеальна, массовые силы консервативны, движение установившееся, имеет место баротропность на линии тока.

Так как жидкость идеальна, то уравнение движения

Так как массовые силы консервативны, то

и уравнение (2.1) можно переписать в виде

(2.3)

Предположение о баротропности на линии тока означает, что

где С постоянна на линии тока.

При установившемся движении траектории и линии тока совпадают. Обозначим через dr(dx,dy,dz) элементарное перемещение вдоль линии тока и умножим скалярно все члены (2.3) на

Так как линия тока является и траекторией, то

Кроме того,

Подставив (2.6) и (2.7) в (2.5), получим

Имея в виду (2.4), введем функцию Р(р, С):

С учетом (2.9) равенство (2.8) можно переписать в виде

(2.11)

Равенства (2.10) и (2.11) имеют место на любой линии тока, но постоянная в правой части (2.11) может изменяться при переходе от одной линии тока к другой.

Равенство (2.11) называют интегралом Бернулли.

Рассмотрим интеграл Бернулли для двух важных случаев.

1. Однородная несжимаемая жидкость. В этом случае - заданная постоянная и . Интеграл Бернулли примет вид

Если массовые силы - силы тяжести, то V = gz и интеграл Бернулли в этом случае

Отдельные слагаемые в (2.14) имеют размерность длины и называются соответственно: - скоростной, z - геометрической, - пьезометрической высотами. Равенство (2.14) позволяет дать такую формулировку интергала Бернулли: при движении однородной несжимаемой жидкости в поле сил тяжести сумма скоростной, пьезометрической и геометрической высот постоянна вдоль линии тока.

2. Совершенный газ. В этом случае уравнение состояния есть уравнение Клапейрона . При сделанных в этой главе предположениях имеет место адиабата Пуассона (1.11). Введем новую постоянную . Тогда

Учитывая (2.15), вычисляем :

Подставив (2.16) в (2.11), получим интеграл Бернулли в виде

Из физики известно, что производная равна квадрату скорости звука. В случае адиабатического процесса можно убедиться, что . Таким образом,

Эта формула является одной из важных формул газовой динамики. В газовой динамике обычно массовые силы не учитывают, а постоянную С обозначают через . В этом случае интеграл Бернулли принимает вид

Здесь v - скорость газа, а - скорость звука в той же точке.

Чтобы определить постоянную в правой части (2.19), достаточно знать характеристики в какой-либо одной точке линии тока. Из (2.19) следует, что скорость звука и температура, а с учетом (2.15), и давление и плотность будут максимальными на линии тока в точке, где скорость равна нулю. Эти величины обычно обозначают через и называют параметрами адиабатически заторможенного газа (параметрами торможения) . Величину называют энтальпией (теплосодержанием). Соответственно постоянную в правой части интеграла (2.19) называют энтальпией торможения. Положив в (2.19) скорость , получим выражение для через параметры заторможенного газа.